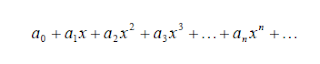La serie de Taylor es una serie funcional y surge de una ecuación en la cual se puede encontrar una solución aproximada a una función. Proporciona una buena forma de aproximar el valor de una función en un punto en términos del valor de la función y sus derivadas en otro punto.
Por supuesto, para hacer esta aproximación sólo se pueden tomar unas cuantas expresiones de esta serie, por lo que el resto resulta en un error conocido como el término residual, es a criterio del que aplica la serie en numero de términos que ha de incluir la aproximación. Pueden resolver por aproximación funciones trigonométricas, exponenciales, logarítmicas etc. La serie de Taylor se basa en ir haciendo operaciones según una ecuación general y mientras mas operaciones tenga la serie mas exacto será el resultado que se esta buscando.
Si esta serie converge para todo x perteneciente al intervalo (a-r, a+r) y la suma es igual a f(x), entonces la función f(x) se llama analítica. Para comprobar si la serie converge a f(x), se suele utilizar una estimación del resto del teorema de Taylor. Una función es analítica si y solo si se puede representar con una serie de potencias; los coeficientes de esa serie son necesariamente los determinados en la fórmula de la serie de Taylor. Si a = 0, a la serie se le llama serie de Maclaurin.
Algunas funciones no se pueden escribir como serie de Taylor porque tienen alguna singularidad. En estos casos normalmente se puede conseguir un desarrollo en serie utilizando potencias negativas de x (véase Serie de Laurent. Por ejemplo f(x) = exp(−1/x²) se puede desarrollar como serie de Laurent.
Donde n! es el factorial de n
F(n) es la enésima derivada de f en el punto a Como se puede observar en la ecuación, hay una parte en la cual hay que desarrollar un binomio (x-a) n por lo que para simplificar el asunto se igualara a "a" siempre a 0. Para fines prácticos no afecta mucho en el resultado si se hacen muchas operaciones en la serie. Teorema de Taylor: Si la función f y sus primeras n+1 derivadas son continuas en un intervalo que contiene a a y a x, entonces el valor de la función en un punto x está dado por:
La expansión en series de Taylor de n-ésimo orden debe ser exacta para un polinomio de n-ésimo orden. Para otras funciones continuas diferenciables, como las exponenciales o sinusoidales, no se obtiene una estimación exacta mediante un número finito de términos.
El valor práctico de las series de Taylor radica en el uso de un número finito de términos que darán una aproximación lo suficientemente cercana a la solución verdadera para propósitos prácticos. ¿Cuántos términos se requieren para obtener una “aproximación razonable”? La ecuación para el término residual se puede expresar como:
Significa que el error de truncamiento es de orden hn+1. El error es proporcional al tamaño del paso h elevado a la (n+1)-ésima potencia.
Existen series de Taylor para:
- Función exponencial
- Logaritmo natural
Error de Propagación:
Supóngase que se tiene una función f(u). Considere que ũ es una aproximación de u (ũ = u+h, con h tamaño de paso). Por lo tanto, se podría evaluar el efecto de la discrepancia entre u y ũ en el valor de la función.
Función e
Se puede aplicar la ecuación de las series de Taylor como mas sencillo le resulte a cada quien, una de tantas formas la explicare aquí. Lo primero que se hace es derivar unas 3 o 4 veces la función, esto porque algunas funciones empiezan a tener un patrón repetitivo después de cierto numero de derivaciones, como la función e. Después se tiene que sustituir "a" en cada una de las derivadas, pero como se decidió que "a" era 0 se sustituye un 0 en cada derivada y se observa que resultados da.
Esto de sustituir en cada derivada es solo para simplificar la ecuacion de la serie y para darnos una idea de como se comporta la funcion. Una vez que se tiene una idea del comportamiento de la funcion se puede ir empezando a armar la ecuación de la serie.
Con las primeras operaciones que se hicieron al principio se puede ver como se ira llenando la serie mientras mas elementos se le agreguen para que el resultado sea mas preciso.
Todo esto fue para ver como es la serie de la funcion e, ahora para conocer algun resultado simplemente se sustituye en donde quedaron las x y ya esta, por ejemplo:
Función Coseno
Para el coseno el procedimiento es el mismo.
Primero se deriva varias veces la función y se sustituye en valor de "a" en cada una para observar el patrón.
Después se va llenando la serie de Taylor para después hacer una ecuación general:
Por último se desarrolla la ecuación general para cualquier caso: