Donde a es otra constante. De hecho, por el Mathboch de “Aplicaciones de las derivadas” sabemos que este tipo de series reciben el nombre de series de MacLaurin y de Taylor, respectivamente. Una serie de Taylor puede ser reducida a una de MacLaurin mediante el siguiente cambio de variable:
En lo que concierne a la convergencia de series, trataremos sólo las series de MacLaurin puesto que las de Taylor se reducen a las primeras mediante un simple cambio de variable.
• Convergencia de una serie de potencias
Investiguemos la convergencia de una serie de potencias de MacLaurin cualquiera. Asignando un
Valor numérico particular a la variable x , se obtiene una serie que convergirá o divergirá
Dependiendo del valor de la x .
http://www.ugr.es/~fjperez/Ejerc_suc_ser_func_screen.pdf
http://www.monografias.com/trabajos11/traaprox/traaprox.shtml#termposit
http://www.unizar.es/analisis_matematico/analisis1/apuntes/
http://planetmath.org/?op=getobj&from=objects&name=FormalPowerSeries
[1] J. M. Ortega (1990): “Introducción al Análisis Matemático”, Manuales de la Universidad
Autónoma de Barcelona, Bellaterra.
[2] V.A. Kudryasvtsev and B.P. Demidovich (1981): “A brief course of Higher Mathematics”, Mir
Publishers, Moscú, p. 447-459.
[3] T.A. Apostol (1981): “Calculus: Cálculo con funciones de una variable, con una introducción al
álgebra lineal”, Reverté, Barcelona, p. 524-542.
[4] M. R. Spiegel (1970): “Manual de Fórmulas y Tablas Matemáticas”, Serie de Compendios
Schaum, McGraw-Hill, Mexico, p. 110-113.
[5] R. Calm, N. Coll, y M.R. Estela (1992): “Problemas de cálculo”, Micromar, Barcelona, p. 229-249.
[6] R. Courant and F. John (1976): “Introducción al Cálculo y al Análisis Matemático”, Limusa,
México, p. 459-463.
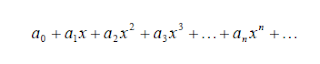






Play Casinos Near Santa Barbara (CA) - Mapyro
ResponderEliminarA map showing casinos and 광명 출장안마 other 포항 출장안마 gaming facilities located near Santa Barbara 부산광역 출장마사지 (CA) casinos, located in the city of Santa Barbara, 영주 출장샵 California, United States. 수원 출장샵